
At work I needed to generate random numbers following a combination of two gaussian distributions – which gave me some headache until someone pointed me to using a Monte Carlo approach. Here’s how.
Typically, any programming language provides some way to generate uniformly distributed random numbers, typically in the interval [0,1]. A histogram of the values looks like this:
However, I needed random numbers following the joint distribution of two gaussian distributions. The histogram should look like this:
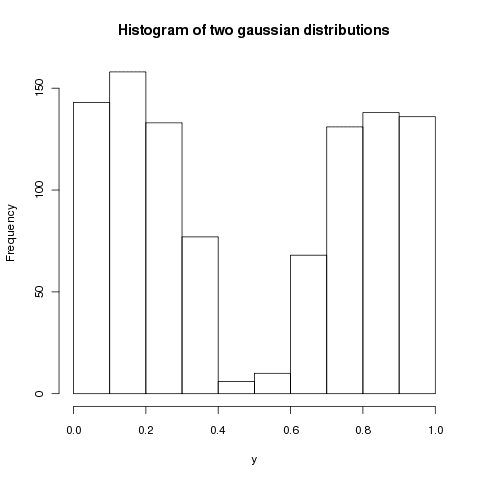
It turns out that it is rather simple to generate random numbers from an given probability density function (PDF) f(x). The only restriction is that there exists another density function g(x) such that c*g(x) majorizes the density function f(x):
c*g(x) >= f(x) for all x.
The steps are rather simple – to generate a random variate x with density f(x):
- Generate x with PDF g(x)
- Generate y uniform on [0, cg(x)]
- If y <= f(x), then output x and return – otherwise repeat from step 1.
Please note that this approach is applicable to many PDFs, but it can be rather slow, depending on the “hit rate”. The algorithm is simple: You generate two uniform random numbers, x and y. Then, you check if y < f(x) – if true, add x to your collection of random numbers. Otherwise, discard it. Repeat the steps until you have enough random numbers. This method is also called Rejection Sampling and was first described by John von Neumann. Other techniques include Inverse Transformation, Composition and Convolution.
I highly recommend reading Chapters 28 and 29 of Rai Jain’s “The Art of Computer Systems Performance Analysis” which outline techniques for generating random numbers of several distributions.
My ruby implementation consists of a MC wrapper and blocks compute the random variate. Currently, I can create gaussian distributions, exponential distributions and a combination of two gaussian distributions. The toolbox also contains a method to scale the range of the random numbers using a linear transformation approach.
[viewcode]src=statistics.rb [/viewcode]
HTML code generated by vim-color-improved v.0.4.0.Download this code: statistics.rb
The title picture was CCed by Saffana, thanks!